Une astuce érgonomique très répondue est la création des menus. Elle souvent utilisée lorsque le programme fait plusieurs choses (plusieurs traitements).
Pour réaliser un menu, il nous faut the structures de contrôle :
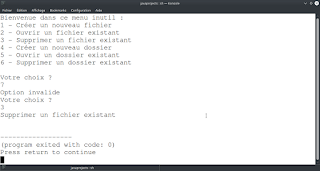
L'exécution sera :
Note : l'édition et l'exécution sont faites sous Geany (site officiel), il garde la fenêtre ouverte et vous donnera des informations sur le déroulement de l'exécution.
Pour réaliser un menu, il nous faut the structures de contrôle :
- Une structure Case ... of (switch en Java) : cette structure permet d'exécuter le traitement adéquat au choix effectué par l'utilisateur.
- Une boucle Répéter ... Jusqu'à pour garantir que l'utilisateur fera un choix valide (principe par ici).
Program Menu; Const MIN = 1; MAX = 6; Var option : Integer; Begin WriteLn('Bienvenue dans ce menu inutil :'); WriteLn('1 - Créer un nouveau fichier'); WriteLn('2 - Ouvrir un fichier existant'); WriteLn('3 - Supprimer un fichier existant'); WriteLn('4 - Créer un nouveau dossier'); WriteLn('5 - Ouvrir un dossier existant'); WriteLn('6 - Supprimer un dossier existant'); WriteLn(); Repeat WriteLn('Votre choix ?'); ReadLn(option); Case (option) of 1 : WriteLn('Créer un nouveau fichier'); 2 : WriteLn('Ouvrir un fichier existant'); 3 : WriteLn('Supprimer un fichier existant'); 4 : WriteLn('Créer un nouveau dossier'); 5 : WriteLn('Ouvrir un dossier existant'); 6 : WriteLn('Supprimer un dossier existant'); else WriteLn('Option invalide'); End; Until ((option >= MIN) And (option <= MAX)); End.
L'exécution sera :
Note : l'édition et l'exécution sont faites sous Geany (site officiel), il garde la fenêtre ouverte et vous donnera des informations sur le déroulement de l'exécution.